
Barbican Consulting Limited
Option Basics

What is an option?
There are two types of option. The first is a call option. The owner of a call option has the right to buy, (but not the obligation to buy). The second is a put option. The owner of a put option has the right to sell, (but not the obligation to sell).
You can either buy or sell options so there are four classic option "positions", they are:
Long call
Short call
Long put
Short put
When we trade options we need to add a little more detail in order to describe exactly what we have done. Let's look at a bond option.
The long call position
Suppose a dealer purchases a call option on a bond. The option will be related to a specific bond known as the underlying. The call option will give the dealer the right to buy a certain amount of that bond on a future date. This is known as the option expiry date. On the expiry date the dealer must decide whether to exercise the option. If exercised the dealer buys the bond at a pre-agreed price known as the strike. If the option is not exercised it expires worthless.
The following details may clarify this explanation:
Long call option:
Underlying: ABC bond, 5% coupon, 2009
Strike: 102%
Expiry: 3 months
When will the trader exercise this option?
The option will be exercised in 3 months time only if the bond has a market value that is greater than 102%. Suppose the market value was 103%. The trader would exercise the option and "call" the bond paying 102%. The bond could now be sold for 103% pocketing the trader a profit of 1%.
On expiry if the underlying price exceeds the strike the trader makes money. The higher the underlying price the greater the profit.
The short call position
For every buyer there is a seller. The person who sells the call option is "short". Whereas the call option buyer has the right to buy the underlying bond at the strike price, the call option seller is obligated to sell the underlying bond at the strike price.
The higher the underlying price at expiry the greater the potential loss for the call option seller. For example, if the strike is 102% and the underlying price is 103% the seller will be called upon to deliver the bond for a price of 102% rather than the market value of 103%. The seller will incur a loss of 1%.
The long put position
Now let's turn our attention to a put option on this bond, here is an example:
Long put option:
Underlying: ABC bond, 5% coupon, 2009
Strike: 98%
Expiry: 3 months
Buying this put option would give you the right but not the obligation to sell the underlying bond at a price of 98% on the expiry date that occurs in 3 months time. How could you benefit? You could benefit if the underlying price was beneath the strike price. Suppose the underlying price was 97%. You could buy the bond for 97%, exercise the option and deliver the bond to the option seller for a price of 98%. You would gain 1%. The option seller would lose 1%. You gain as the market price of the bond falls.
The short put position
Whereas the put option buyer has the right to sell the underlying bond at the strike price, the put option seller is obligated to buy the underlying bond at the strike price.
The lower the underlying price at expiry the greater the potential loss for the put option seller. For example, if the strike is 98% and the underlying price is 97% the seller of the option will be required to buy the bond for a price of 98% rather than the market value of 97%, a loss of 1%.
A fundamental difference
Long option positions create profit opportunities, short option positions create potential losses. This is one reason why managers and regulators are particularly nervous of short option positions.
In theory short positions can lead to unlimited losses and therefore need to be managed effectively.
If selling options is this risky why do it?
Because the buyer of the option pays the seller of the option a premium. This is an up-front payment that compensates the seller for the risks that are being taken. The size of this premium will be proportionate to the risk of loss incurred at the time of sale.
How could we use options?
Here are a few very simple strategies that could be adopted:
You expect the bond price will rise-you could buy a call option
You expect the bond price will fall-you could buy a put option
You expect the bond price will rise or remain static-you could sell a put option
You expect the bond price will fall or remain static-you could sell a call option
Whether you benefit from these trades is entirely dependent on how the market moves.
Whilst these strategies can be profitable you may experience losses.
Classic pay-off profiles:
The long call pay-off at expiry:

Losses are limited to the premium payment
Profits increase with a rise in the underlying price
The short call pay-off at expiry:

Maximum profit is the premium payment
Unlimited losses as the underlying price rises
The long put pay-off at expiry:

Losses are limited to the premium payment
Profits increase with a fall in the underlying price
The short put pay-off at expiry:

Maximum profit is the premium payment
Unlimited losses as the underlying price falls
How important are options to you?
There are actively traded option markets for interest rates (caps, floors, swaptions), bonds, foreign exchange and commodities. Some of these are exchange traded, many are over-the-counter derivative contracts.
Optionality also occurs in products that you would not normally associate with options. Here are two specific examples:
1. A bank makes a fixed rate mortgage loan. The normal way to hedge the interest rate risk on this loan is for the bank to pay fixed interest on a swap and receive Libor. The Libor receipt matches the funding cost of the bank.
A proportion of mortgages will be pre-paid during their life. Prepayment often occurs because a mortgage has been refinanced at a lower interest rate. (If interest rates decline it becomes economical for borrowers to refinance their original loan and hence pre-payment rates increase).
Where is the optionality?
Pre-payment leaves the bank with an asset that is shrinking whilst the swap hedge remains unchanged.
The bank needs to cancel part of the swap. But because interest rates have fallen, (and the bank is paying fixed), the bank will incur a breakage cost. Passing this cost on the customer is not always straight forward.
The customer is long the pre-payment option, the bank is short.
2. A bond dealer buys a floating rate note, (FRN). The coupon on this particular FRN has a maximum and a minimum interest rate.
This FRN contains a cap and a floor, these are options on Libor. The dealer is short the cap and long the floor.
If interest rates increase the FRN coupon may reach its maximum. This represents a real cost for the investor and the value of the FRN will be adversely affected.
Valuation of this bond must take into account the value of these options. Dealers who fail to recognise the embedded optionality may be in for an unpleasant surprise.
The key point is that you can find option risks in many areas of business and these risks can cause serious problems if they are not managed effectively.
Here are a few more terms we need to be familiar with before continuing:
American option: an option that can be exercised at any time until the expiry date.
European option: an option that can only be exercised on the expiry date, (the majority of over the counter interest rate options are of this nature).
Bermudan option: an option that can be exercised on several different dates in the future.
In the money option, (ITM): for ITM call options the underlying price is higher than the strike price for ITM put options the underlying price is lower than the strike price. (If you exercised ITM options you would gain).
At the money option, (ATM): an option where the strike price and underlying price are identical.
Out of the money option, (OTM): for OTM call options the underlying price is lower than the strike price for ITM put options the underlying price is higher than the strike price. (If you exercised OTM options you would lose).
What is put call parity?
Put call parity refers to the fact that different option positions can be combined together to create the underlying.
A simple example is as follows:
If you buy an ATM call option on a bond and sell an ATM put option on the same bond you have synthetically created the bond.
If the bond price rises the call option gains. If the bond price falls the short put loses.
In other words option prices should be consistent with the price of the underlying. If not an arbitrage opportunity exists.
What are straddles, strangles and butterflies?
Straddles, strangles and butterflies are names given to option strategies that traders employ.
Traders can use different combinations of calls and puts to create bespoke pay off profiles. These profiles make money in accordance with a trader's expectations.
For example if the trader expects the underlying price to rise or fall he could buy an ATM call and an ATM put. A combination known as a straddle.
If the underlying price increased or decreased significantly the trader would make money.
But there are no free lunches! If the underlying price remained relatively static the trader would lose both option premium payments.
Where do option prices come from?
For vanilla options that are traded in liquid markets eg caps, floors, swaptions and FX options the market price is observable. In this sense "fair value" can be determined be reference to quoted market prices.
However many trades in the over-the-counter market may not be identical in structure to those quoted by banks or brokers. For example the strike or expiry may differ. This makes the pricing and valuation of options problematic particularly for the end user or customer.
To price and value options banks use mathematical models, (option pricing models). These models have been in existence for 20 - 30 years. Perhaps the most frequently mentioned model is the Black Scholes model and later variations.
The seller of an option is taking a risk, a risk that they will lose money from their action.
The price or option premium compensates them for this risk. In simple terms the premium is the market's estimate of how much money the option seller can expect to lose. Option pricing models provide the monetary value of this risk.
The following is not a rigorous explanation of these models, it is a straight forward explanation of how various inputs used in a model affect the option price.
In order to price an option a dealer inputs information into the pricing model. This information will include whether the option is a call or put, the time to expiry, the underlying price, the strike and the volatility.
These inputs will have a direct effect on the value of the option. You don't have to be an options trader in order to appreciate the effect that these inputs have on price. Here are some simple "rules of thumb".
If you sell longer dated options more time is available for the underlying price to move and for the option to become in-themoney. Longer dated options are more expensive-the seller is taking greater risk.
Out of the money options are less likely to be exercised than atthe-money or in-the-money options. OTM options are therefore cheaper-the seller is taking less risk.
Increasing volatility will increase the probability that an option, (call or put), will expire in the money. Increasing volatility increases the risk the option seller is taking and as a consequence the option premium will rise.
What is volatility & why is it important?
Option traders refer to volatility as a measure of risk. Statisticians refer to annualised standard deviation. This is the dispersion of price around the mean or average, the greater the dispersion the higher the standard deviation or volatility.
In simple terms the more things go up and down in price the higher the volatility. For an option trader this is important. High volatility means that an option has more chance that it will expire in the money and therefore cause the seller to lose money.
Now the tricky bit! There are two types of volatility that we could use in order to price options. The first is historic volatility, the second is implied volatility.
1. Historic volatility is determined by collecting historic price information and calculating the annualised standard deviation. (The sort of exercise you could do using a spread sheet). Historic volatility looks backwards, it is a measure of what happened in the past. For this reason traders do not use historic volatility to price options. Historic volatility does have its use. Risk managers often use it to calculate the probability of loss arising from dealer's positions.
2. Implied volatility is found by re-working the option pricing model. Instead of solving to find the option price we use the market price of the option as one of the inputs, (together with time, strike, underlying price etc) and solve in order to find the volatility. In other words what risk does the market price imply?
Implied volatility is used by traders to price options. This may sound complicated but it is logical.
If you trade options you want to make prices based on the current market price for risk not the historic measurement of risk.
For non-traders implied volatility can cause difficulties. Let's suppose you want to independently value the option positions that a trader has.
You obtain the appropriate option pricing model, input the relevant information but what implied volatility do you use? You may find a suitable independent data source that provides you with the implied volatility you need. But this can be difficult for instruments and markets that are less liquid.
It is also a well known fact that puts and calls can trade with different volatilities and options with strikes that are OTM, ATM and ITM options can trade with different implied volatilities. (This technical issue with option pricing has very important valuation implications which are beyond this introduction).
What are the Greeks?
Greek letters are used by option traders and risk managers. The Greeks describe the risk of an option position and are therefore important in determining limits, hedging and trading strategies. The Greeks are:
Delta
An option's delta is its sensitivity to small changes in the price of the underlying. Deltas are used for basic hedging ratios, this is explained later.
A deep in the money option has a delta approximating at 1. When the underlying price changes the value of this option changes by a similar amount-it behaves like the underlying.
ATM options have deltas of 0.5. A 1% change in the underlying price will change the option value 0.5%. A deeply OTM has a delta approaching zero, (see diagram below).

Gamma
When the underlying price changes the option delta changes, but the rate of change is not constant. Gamma refers to the rate of change of the delta. We will see that this has important implications.
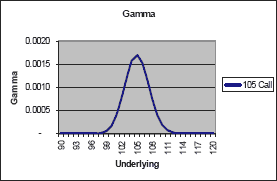
Gamma is a problem for traders, particularly if they are "delta hedging" option positions, (see opposite). Low gamma positions are easier to hedge because the hedge ratio is not subject to such large adjustments.
Theta
Theta describes how the value of an option decays with time. As an option matures its time value declines at an increasing rate. Short dated options in particular suffer rapid time decay as they reach expiry.
Vega or Lambda
This is the sensitivity of the option to changes in implied volatility. Long option positions are positive vega, that means if volatility rises they increase in value. By way of contrast short option positions have negative vega.
What is delta hedging?
The delta is a very simple hedge ratio. For example suppose a trader sells a $10m bond call where the strike and underlying bond price are both 100%. If we assume that on expiry of the option the bond price has a 50% probability it is higher than par and a 50% probability it is lower than par. The option delta is 0.5. This means in order to hedge the short call position the trader must buy $10m x 0.5 = $5m of the bond.
If the bond price increases the delta increases, if it falls the delta declines. The trader must continually rebalance the hedge to reflect the change in the delta.
Unfortunately for the trader if the delta increases he buys more of the bond at higher and higher prices. If the delta falls he sells part of his position at lower and lower prices. In other words rebalancing is necessary but it is expensive. If the premium income received fails to cover the hedging cost this trader will lose money.
At the money options with short maturities to expiration are particularly sensitive to small changes in the underlying price. Delta hedging these options is difficult, one minute they are going to expire ITM with a delta of 1 a moment later they are going to expire worthless with a delta of zero. They have high gamma, (see gamma diagram above).
Interest rate options: caps, floors & swaptions
Caps and floors are options on short term interest rates, (Libor). Swaptions are options on long term interest rates, (swaps).
How caps work: A typical cap will have a maturity date of between 2 and 10 years. It will also have a strike which is expressed as an interest rate. Suppose a 2 year cap has a strike of 7.00%. Every 3 months the parties to the trade "capture" 3 month Libor. If this rate is greater than the strike the seller of the cap pays the buyer of the cap a sum of money.
Suppose Libor fixed at 7.50% and the nominal amount of the trade was $10m. This amount would be 10m x 0.50% x 91/360 = $12,638.89.
This process is repeated every 3 months during the life of the cap. Every time Libor exceeds the strike there is a payment from the cap seller to the cap buyer. A cap is therefore not one option but a string of individual options known as "caplets" on forward Libor rates.
What can a cap be used for? One simple use for a cap is hedging interest rate risk, in particular exposures to rising short term interest rates. Typically a borrower with a floating rate liability may use a cap to provide a ceiling on interest servicing costs if rates increase.
For this protection the buyer of the cap will pay the seller a premium. For caps this is a one off upfront premium payment normally expressed in basis points, (bp). For example if a cap cost 25 bp, $10m nominal would cost $25,000.
How is the premium cost determined? Simply it is the market's current price of the risk that the option seller is running. Traders use an option pricing model, (Black model), to price these options. To recap various inputs are required, their effect on the option premium is as follows:
Time: Longer dated caps present the option seller with a greater probability that they will lose money-the option premium is therefore higher.
Strike: The lower the strike the greater the probability that the caplets will expire in the money. Lower strikes therefore increase the option premium.
Forward rates: It is the relationship between the forward Libor rates and the strike that determine whether individual caplets are in, at or out of the money. Rising forward rates will increase the price of the cap, falling forward rates will decrease the cost.
Implied volatility: Increasing implied volatility increases the risk for the cap seller. There is more chance that the option will expire in the money. Increased volatility will therefore make the cap more expensive.
How floors work: A floor will typically have a maturity date of between 2 and 10 years. It will also have a strike which is expressed as an interest rate. Suppose a 2 year floor has a strike of 4.00%. Every 3 months the parties to the trade "capture" 3 month Libor. If this rate is lower than the strike the seller of the floor pays the buyer a sum of money.
Suppose Libor fixed at 3.50% and the nominal amount of the trade was $10m. The amount would be 10m x 0.50% x 91/360 = $12,638.89. This process is repeated every 3 months during the life of the floor.
Each time Libor is beneath the strike there is a payment from the floor seller to the floor buyer. A floor is therefore not one option but a string of individual options known as "floorlets" on forward Libor rates.
What can a floor be used for? One simple use for a floor is to hedge interest rate risk, in particular exposures to falling short term interest rates. Typically an investor with a floating rate asset may buy a floor to provide a minimum investment return on an investment that is linked to Libor.
Reducing premium costs
Many cap and floor buyers don't like paying the option premium. One obvious way to reduce the premium cost is to buy options that are out of the money. For example if forward interest rates are rising a cap with strikes that periodically rise will reduce the option premium.
Another way to reduce the premium payment is to use combinations of options. A collar is one such structure. With a collar the cap buyer simultaneously sells a floor. For a floating rate borrower this means there is a maximum borrowing cost, (cap strike) and a minimum borrowing cost, (floor strike). If the cap premium equals the floor premium there is no net premium payment. This structure is sometimes referred to as a "zero cost collar".
Swaptions
As the name suggests a swaption is an option on a forward starting swap. There are two types of swaption.
1. A payer's swaption: this allows te option buyer to exercise the option and enter into a swap to pay fixed interest*. Here is an example. A swaption buyer purchases a payer's swaption with the right to pay fixed interest in 2 years time at 7% on a 3 year swap.
If in 2 years time the then 3 year swap rate is higher than 7% the buyer will exercise the option, (7% is better than the market rate, this swap is in-the-money).
2. A receiver's swaption: this allows the option buyer to exercise the option and enter into a swap to receive fixed interest*. Here is an example. A swaption buyer purchases a receiver's swaption with the right to receive fixed interest in 2 years time at 7% on a 3 year swap. If in 2 years time the then 3 year swap rate is lower than 7% the buyer will exercise the option, (7% is better than the market rate, this swap is in-the-money).
*The swaption can be settled physically, (exercising the swaption leads to a real swap), or cash settled, (the profit on the trade is paid to the swaption buyer by the seller and no swap is subsequently entered into). The method of settlement is agreed between the buyer and seller when the swaption is initially traded.
What can swaptions be used for?
Swaptions have a variety of practical uses. For example a 5 year fixed rate loan may have a further 2 year extension period that the borrower can exercise in year 5. If interest rates have risen the borrower may extend the loan in year 5. How can the bank hedge this risk? The bank can buy a payers swaption. This swaption will allow the bank to pay fixed interest on a swap in 5 years time for a period of 2 years.
First Published by Barbican Consulting Limited 2007